Questionbang mock-set-plus is a premier assessment platform for various competitive exams including NEET, JEE and Bank exams. The application offers a feature to provide feedback once a user attempts a free mock exam. These reviews are captured and recorded through TrustSpot.
As a part of internship, I wanted to use machine learning (ML) to decide whether a user is a potential reviewer and be insisted for a feedback.
Importance of user reviews
The success of any application depends on how it meets user expectations. It is vital for any application to constantly evolve to address changing user requirements and expectations. This can be possible only by gathering regular reviews from the user community.
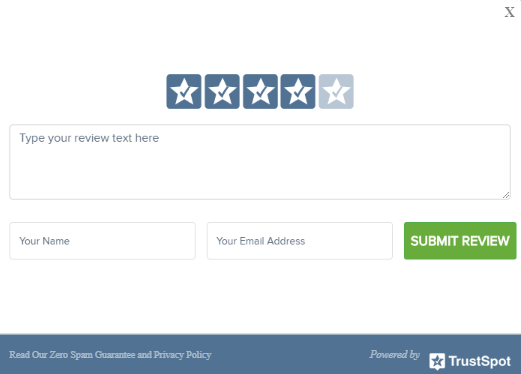
Every topic in mock-set-plus has a free mock exam. These are of short duration. Most users who visit mock-set-plus attempt free papers to have a quick overview of online mock exams. They are asked to give a feedback and a star rating immediately after completing the exam session.
Figure 1. mock-set-plus asking for TrustSpot reviews.
Not many users give feedback or rating, they simply skip over to the next stage for reviewing results. Now, whether a user be reminded to give feedback? It is not going to be a good user experience, if an application regularly asks users for reviews or other feedback. So, we need to be careful while seeking second time for the review. To make this process restrained, we wanted to classify users based on whether they are potential reviewers or not.
Scenario 1
A user who hardly attempted questions, ends a session without giving any feedback.
Scenario 2
A user who does extremely well with an exam, but skips over without giving feedback.
In scenario (1), let us assume, the user did not like any of the questions or the user felt the mock exam is not worthy of attempting. But, a feedback on why the application has been disliked, can be a valuable input. We should insist such a user for a feedback.
In scenario (2), the user might have found the questions to be obvious or ordinary. The application would really benefit by having this feedback.
In short, every user can be a source of valuable feedback. The only concern now is whether a user be insisted to give a feedback?
Let us use historical data from TrustSpot reviews to decide whether a user is a potential reviewer.
| User | Q attempted (Q) |
Time spent (T) in minutes |
Score (S) |
Reviewed or not |
|---|---|---|---|---|
| Sonal S | |
|
|
Yes |
| krishna | |
|
|
No |
| Meghana R | |
|
|
Yes |
| Pooja Thathera | |
|
|
No |
| Akanksha Bangera | |
|
|
Yes |
| Rajesh Gaddanaker | |
|
|
Yes |
| guruprasad | |
|
|
No |
| Illa Durgesh | |
|
|
Yes |
| Murali Manohar | |
|
|
Yes |
| Sandip Ingle Thakur | |
|
|
No |
| Niranjan Kannanugo | |
|
|
Yes |
| koushik | |
|
|
Yes |
| Isabella Dawn | |
|
|
No |
| Sachith Jaugar | |
|
|
Yes |
| Asad Inamdar | |
|
|
Yes |
| Sweety S | |
|
|
No |
| ramdas gavit | |
|
|
Yes |
Table 1: A table showing snapshots of free mock exam sessions and TrustSpot reviews.
Choosing a ML technique – whether a user is a potential reviewer?
Our requirement is to assess whether a user will rate mock-set-plus on TrustSpot. What we have is historical ratings from TrustSpot. As we can see above, there are multiple factors (probably dependent) that contribute in a user’s decision to rate or not.
– How many questions user attempted?
– How much time a user has spent?
– What is the score?
The requirement for now is to connect historical trend to compute a probability of an outcome. We will use Naive-Bayes technique.
Preprocessing
Let us categorize above data (table 1) into the following groups:
- Total number of questions attempted –
Low: if it is less than or equal to 50%,
High: if it is more than 50%.
- Total time spent –
Low: if it is less than or equal to 50%,
High: if it is more than 50%.
- Score –
Low : if it is less than or equal to 50%,
High: if it is more than 50%.
Table of preprocessed data with low and high values:
| User | Q attempted (Q) |
Time spent (T) |
Score (S) |
Reviewed or not |
|---|---|---|---|---|
| Sonal S | High | High | Low | Yes |
| krishna | Low | Low | Low | No |
| Meghana R | High | High | Low | Yes |
| Pooja Thathera | High | Low | High | No |
| Akanksha Bangera | High | Low | Low | Yes |
| Rajesh Gaddanaker | High | High | Low | Yes |
| guruprasad | High | Low | High | No |
| Illa Durgesh | High | Low | High | Yes |
| Murali Manohar | High | High | Low | Yes |
| Sandip Ingle Thakur | Low | Low | Low | No |
| Niranjan Kannanugo | High | Low | Low | Yes |
| koushik | High | Low | High | Yes |
| Isabella Dawn | High | High | Low | No |
| Sachith Jaugar | High | Low | Low | Yes |
| Asad Inamdar | High | High | Low | Yes |
| Sweety S | High | High | Low | No |
| ramdas gavit | High | High | High | Yes |
Table 2: Table showing classification of features.
Using Naive Bayes classifier to identify potential reviewers
Naive Bayes is a statistical classification technique based on Bayes Theorem. The classifier assumes that the effect of a particular feature in a class is independent of other features. In our case, the features Q, S and T can have some role in a rating event. As per Naive-Bayes classifier, these features are assumed to be independent while computing probability. This assumption simplifies the computation, and that’s why it is considered as naive.
![]()
![]()
- P(h): the probability of hypothesis h being true (regardless of the data). This is known as the prior probability of h.
- P(D): the probability of the data (regardless of the hypothesis). This is known as the prior probability.
- P(h|D): the probability of hypothesis h given the data D. This is known as posterior probability.
- P(D|h): the probability of data d given that the hypothesis h was true. This is known as posterior probability.
In our case,
likelihood of giving a review
![]()
![]()
likelihood of not giving a review
![]()
![]()
Next, let us check whether a user will rate based on following inputs:
Total questions attempted ![]()
![]()
![]()
![]()
Total marks scored ![]()
![]()
![]()
![]()
Total time taken ![]()
![]()
![]()
![]()
For above condition,
likelihood of giving a review
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
likelihood of not giving a review
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For above condition there is 87% chance that the user is going to rate mock-set-plus.
Final thoughts
As the application is going to constantly accumulate rating data, the prediction accuracy may improve over a period of time. More importantly, how accurate, these predictions in a production setup are something to watch for.
The classification of features (Q, T, S) for now is very broad (low/high) based. Ideally, this should be on a wider scale, e.g., poor, low, average, good, excellent, or something similar. This is something, we hope can achieve better accuracy in predictions.
Lastly, I would like to thank Questionbang team, esp., Raksha Raikar for all the guidance and help throughout the internship.
References:
- mock-set-plus
- Questionbang TrustSpot reviews
- Trackthrough – an online software for planning, tracking and monitoring activities of a project.
- JEE 360 app reviews
- NEET Weekly app reviews
- CET Social app reviews
- Bank Preparatory app reviews
- Questionbang apps
- http://users.sussex.ac.uk/~christ/crs/ml/lec02b.html